BAB I
PENDAHULUAN
A. LATAR BELAKANG
Pendidikan adalah usaha sadar yang sengaja dirancang untuk mencapai tujuan yang telah ditetapkan. Pendidikan bertujuan untuk meningkatkan kualitas sumber daya manusia. Pendidikan merupakan salah satu cara pembentukan kemampuan manusia untuk menggunakan rasional seefektif dan seefisien mungkin sebagai jawaban dalam menghadapi masalah-masalah yang timbul dalam usaha menciptakan masa depan yang baik
Yuwono dalam Sudarsiah (2005:1), mengemukakan bahwa sudah banyak usaha yang dilakukan oleh pemerintah untuk meningkatkan kualitas pendidikan di Indonesia, khususnya kualitas pendidikan matematika di sekolah, namun belum menampakkan hasil yang memuaskan, baik ditinjau dari proses pembelajarannya maupun dari hasil prestasi belajar siswanya.
Matematika sebagai salah satu mata pelajaran di sekolah dinilai sangat memegang peranan penting karena matematika dapat meningkatkan pengetahuan siswa dalam berpikir secara logis, rasional, kritis, cermat, efektif, dan efisien. Oleh karena itu, pengetahuan matematika harus dikuasai sedini mungkin oleh para siswa.
Kebanyakan proses pembelajaran yang digunakan oleh guru adalah pembelajaran konvensional (pembeljaran yang dilakukan guru disekolah pada umumnya) yakni ceramah, tanya jawab dan pemberian tugas. Berdasarkan observasi langsung di lapangan pada tanggal 1 September 2007 diperoleh data berupa prestasi belajar matematika siswa Kelas VII SMP Negeri 8 Kendari pada semester 1 tahun 2006 yaitu 5,2 ketuntasan secara klasikal yang belum mencapai standar minimal yaitu 6,00. Hal tersebut diakibatkan karena kurang aktifnya mental fisik siswa dalam proses belajar mengajar, dimana pendekatan pembelajaran yang digunakan adalah pendekatan pembelajaran Konvensional. Dalam hal ini, proses belajar-mengajar didominasi oleh guru. Oleh karena itu, pendekatan pembelajaran tersebut perlu segera dirubah.
Soedjadi dalam Sudarsiah (2005:2) mengemukakan bahwa, di negeri Belanda telah dikembangkan Pembelajaran Matematika Realistik (PMR). Dalam pendekatan PMR, pembelajaran matematika lebih memusatkan kegiatan belajar pada siswa dan lingkungan serta bahan ajar yang disusun sedemikian sehingga siswa lebih aktif mengkonstruksi atau membangun sendiri pengetahuan yang akan diperolehnya.
Melalui PMR yang pengajarannya berangkat dari persoalan dalam dunia nyata, diharapkan pelajaran tersebut menjadi bermakna bagi siswa. Dengan demikian mereka termotivasi untuk terlibat dalam pelajaran. Untuk mendukung proses pembelajaran yang mengaktifkan siswa diperlukan suatu pengembangan materi pelajaran matematika yang difokuskan kepada aplikasi dalam kehidupan sehari-hari (kontekstual) dan disesuaikan dengan tingkat kognitif siswa, serta penggunaan metode evaluasi yang terintegrasi pada proses pembelajaran.
Dalam PMR pembelajaran tidak dimulai dari defenisi, teorema atau sifat-sifat kemudian dilanjutkan dengan pembahasan contoh-contoh, seperti yang selama ini dilaksanakan diberbagai sekolah. Namun sifat-sifat, definisi, cara, prinsip, dan teorema diharapkan seolah-olah ditemukan kembali oleh siswa melalui penyelesaian kontekstual yang diberikan guru di awal pembelajaran. Dengan demikian dalam PMR siswa didorong atau ditantang untuk aktif bekerja, bahkan diharapkan dapat mengkonstruksi atau membangun sendiri pengetahuan yang diperolehnya (Dalyana, 2003:17).
Berdasarkan pemikiran tersebut, maka penulis mencoba melakukan penelitian yang berjudul : “Efektivitas Pendekatan Pembelajaran Matematika Realistik Dalam Meningkatkan Kemampuan Penalaran Matematika Siswa Kelas VII SMP Negeri 8 Kendari”.
B. BATASAN MASALAH
Masalah dalam penelitian ini dibatasi hanya pada pelaksanaan Pendekatan Pembelajaran Matematika Realistik meningkatkan kemampuan penalaran matematika siswa dalam proses belajar-mengajar matematika kelas VII Semester 1 SMP Negeri 8 Kendari Tahun Ajaran 2007/2008 Khusus Pokok Bahasan Perbandingan.
C. RUMUSAN MASALAH
Berdasarkan uraian pada latar belakang di atas, maka masalah dalam penelitian ini dirumuskan sebagai berikut:
1. Bagaimanakah kemampuan penalaran matematika siswa kelas VII SMP Negeri 8 Kendari yang diajar dengan pendekatan pembelajaran matematika realistik?
2. Bagaimanakah kemampuan penalaran matematika siswa kelas VII SMP Negeri 8 Kendari yang diajar tanpa pendekatan pembelajaran matematika realistik?
3. Apakah penerapan pendekatan pembelajaran matematika realistik (PMR) lebih efektif dibandingkan dengan pendekatan pembelajaran konvensional dalam meningkatkan kemampuan penalaran matematika siswa kelas VII SMP Negeri 8 Kendari?
D. TUJUAN PENELITIAN
Sejalan dengan rumusan masalah diatas, tujuan penelitian ini adalah untuk:
1. Mendiskripsikan efektifitas pembelajaran matematika realistik (PMR) dalam kemampuan penalaran matematika Siswa Kelas VII SMP Negeri 8 Kendari.
2. Mendiskripsikan efektifitas penerapan Pendekatan Pembelajaran Matematika Realistik (PMR) dengan pendekatan pembelajaran konvensional dalam meningkatkan kemampuan penalaran Siswa Kelas VII SMP Negeri 8 Kendari.
E. MANFAAT PENELITIAN
1. Sebagai bahan informasi bagi guru tentang kemampuan penalaran matematika yang dimiliki siswa.
2. Sebagai bahan informasi bagi sekolah dalam upaya peningkatan mutu pendidikan khususnya pendidikan matematika.
3. Sebagai bahan referensi bagi peneliti selanjutnya.
BAB II
KAJIAN PUSTAKA
A. Efektivitas Pembelajaran
Efektivitas pembelajaran berarti tingkat keberhasilan. Menurut Popham (2003:7) Efektivitas pengajaran seharusnya ditinjau dari hubungan guru tertentu yang mengajar kelompok siswa tertentu, di dalam situasi tertentu dalam usahanya mencapai tujuan-tujuan instruksional tertentu.
Dunne (1996:12) berpendapat bahwa Efektivitas pembelajaran memiliki dua karakteristik. Karakteristik pertama ialah ”memudahkan murid belajar” sesuatu yang ”bermanfaat”, seperti fakta keterampilan, nilai, konsep dan bagaimana hidup serasi dengan sesama, atau sesuatu hasil belajar yang diinginkan. Karakteristik kedua, bahwa keterampilan diakui oleh mereka yang berkompeten menilai, seperti guru-guru, pelatih guru-guru, pengawas, tutor dan pemandu mata pelajaran atau murid-murid sendiri.
Selanjutnya konsep keefektifan pengajaran dikaitkan dengan peranan guru sebagai pengelola proses belajar-mengajar, bertindak selaku fasilitator yang berusaha menciptakan kondisi belajar-mengajar yang efektif sehingga memungkinkan proses belajar-mengajar, mengembangkan bahan pelajaran dengan baik, dan meningkatkan kemampuan siswa untuk menyimak pelajaran dan menguasai tujuan-tujuan pendidikan yang harus mereka capai (Usman, 2000:21).
Berdasarkan pendapat di atas, maka sehubungan dengan penelitian ini, efektivitas pembelajaran adalah suatu keadaan yang menunjukkan sejauh mana apa yang telah direncanakan dapat tercapai. Semakin banyak rencana yang dapat dicapai, semakin efektif pula kegiatan tersebut, sehingga kata efektivitas dapat pula diartikan sebagai tingkat keberhasilan. Dengan demikian pengertian efektivitas dalam penelitian ini adalah sejauh mana Pembelajaran Matematika Realistik efektif digunakan dalam meningkatkan kemampuan penalaran matematika siswa.
B. Kemampuan Penalaran Matematika
Sumarmo dalam Fahinu (2007:4) mengemukakan bahwa kemampuan penalaran matematika adalah suatu kemampuan yang muncul dalam bentuk: 1) menarik kesimpulan secara logik, 2) menyusun dan menguji konjektur, menyusun pembuktian langsung, tak langsung, dan menggunakan induksi matematik, 3) merumuskan lawan contoh (counter examples), dan 4) menyusun argumen yang valid. Kemampuan koneksi matematik misalnya muncul dalam bentuk: memahami representasi ekuivalen konsep yang sama.
Pentingnya kemampuan penalaran dalam pembelajaran matematika juga dikemukakan oleh Suryadi dalam Saragih (2007:4) yang menyatakan bahwa pembelajaran yang lebih menekankan pada aktivitas penalaran dan pemecahan masalah sangat erat kaitannya dengan pencapaian prestasi siswa yang tinggi. Sebagai contoh pembelajaran matematika di Jepang dan Korea yang lebih menekankan pada aspek penalaran dan pemecahan masalah mampu menghasilkan siswa berprestasi tinggi dalam tes matematika yang dilakukan oleh TIMSS.
Berpikir kritis dalam belajar matematika merupakan suatu proses kognitif atau tindakan mental dalam usaha memperoleh pengetahuan matematika berdasarkan penalaran matematis. Penalaran matematis meliputi menarik kesimpulan logis; memberikan penjelasan dengan menggunakan model, fakta, sifat-sifat, dan hubungan untuk menganalisis situasi matematis; menarik analogi dan generalisasi; menyusun dan menguji konjektur; memberikan lawan contoh (counter example); mengngikuti aturan inferensi memeriksa validitas argumen; menyusun argumen yang valid; menyusun pembuktian langsung, tak langsung dan menggunakan induksi matematis.
C. Hakekat Belajar Matematika
Belajar matematika merupakan proses psikologis, yaitu berupa kegiatan aktif dalam upaya memahami dan menguasai konsep matematika. Kegiatan aktif dimaksudkan adalah pengalaman belajar matematika yang diperoleh siswa melalui interaksi dengan matematika dalam konteks belajar mengajar di lembaga pendidikan formal.
Dalam dunia pendidikan sekarang ini menganggap bahwa belajar sebagai suatu proses dimana menyebabkan perubahan-perubahan tingkahlaku berkat pengalaman dan latihan. Hal ini sejalan dengan pendapat yang dikemukakan oleh beberapa ahli psikologi, yang dikutip oleh Purwanto dalam Tati Andriyati (2006:8), sebagai berikut:
1. Hilgard dan Bower mengemukakan, belajar berhubungan dengan perubahan tingkahlaku seseorang terhadap sesuatu situasi tertentu yang disebabkan pengalamannya yang berulang-ulang dalam situasi itu, dimana perubahan tingkahlaku itu dapat dijelaskan atas dasar kecenderungan respon bawaan, kematangan atau keadaan-keadaan sesaat seseorang.
2. Morgan mengemukakan, belajar adalah setiap yang relatif menetap dalam tingkahlaku yang terjadi sebagai suatu hasil dari latihan atau pengalaman.
Matematika adalah merupakan ilmu yang berhubungan dengan penelaahan bentuk-bentuk atau struktur yang abstrak dan hubungan antara hal-hal tersebut. Untuk dapat memahami struktur dan hubungan-hubungannya diperlukan penguasaan tentang konsep-konsep yang terdapat dalam matematika. Hal ini berarti matematika merupakan belajar konsep dan struktur yang terdapat dalam bahan yang sedang dipelajari, serta mencari hubungan antara konsep dan struktur (Karso, 1998: 40).
Dalam Mempelajari matematika perlu diketahui karakteristik matematika. Menurut Hudoyo dalam Roslina (2005:15) karakteristik yang dimaksud antara lain (1) Dalam matematika banyak kesepakatan dan penalaran, (2) Sangat dipertahankan adanya konsistensi atau taat asas, (3) Obyek matematika bersifat abstrak, (4) Susunan atau struktur matematika bersifat hirarkis, (5) Penalaran dalam matematika bersifat deduktif atau aksiomatik.
Dari uraian di atas dapat dikatakan bahwa belajar matematika pada hakekatnya adalah merupakan kegiatan psikologis, yakni kegiatan aktif dalam memahami dan menguasai serta mengkaji berbagai hubungan antara obyek-obyek matematika sehingga diperoleh pengetahuan baru atau peningakatan pengetahuan.
D. Pembelajaran Matematika Realistik (PMR)
Marpaung dalam Fahinu (2005:1) mengemukakan bahwa faktor yang menyebabkan nilai matematika rendah adalah paradigma proses pembelajaran matematika di kelas memiliki ciri-ciri: a) guru aktif menyampaikan sejumlah informasi; b) siswa “dipaksa” belajar, tidak menumbuhkan kesadaran makna belajar; c) pembelajaran berfokus kepada guru; d) ketergantungan siswa pada guru; e) kompetensi siswa kurang diperhatikan dan dikembangkan; f) pemahaman materi yang dipelajari diukur melalui tes objektif; g) kesempatan siswa melakukan refleksi dan negosiasi melalui interaksi kurang dikembangkan, dan h) pemahaman siswa cenderung pada pemahaman instrumental bukan pada pemahaman relasional. Akibatnya: siswa tidak mempunyai kesempatan untuk mengembangkan ide-ide kreatif, kurang berkembangannya daya nalar, dan kurang kreatifitas dalam memecahkan masalah.
Salah satu karakteristik matematika adalah mempunyai obyek yang bersifat abstrak. Sifat abstrak ini menyebabkan banyak siswa mengalami kesulitan dalam mempelajari matematika, kurang menghayati dan memahami matematika dan siswa mengalami kesulitan mengaplikasikan matematika dalam kehidupan sehari-hari. Salah satu pendekatan pembelajaran yang berkaitan dengan pengalaman sehari-hari dan menerapkan matematika dalam kehidupan sehari-hari adalah Pembelajaran Matematika Realistik (PMR).
Pembelajaran Matematika Realistik (PMR) pada dasarnya adalah pemanfaatan realitas dan lingkungan yang dipahami peserta didik untuk memperlancar proses pembelajaran matematika sehingga dapat mencapai tujuan pendidikan matematika secara lebih baik daripada masa yang lalu. Dalam pandangan PMR, pengembangan suatu konsep matematika dimulai oleh siswa secara mandiri berupa kegiatan eksplorasi sehingga memberikan peluang pada siswa untuk berkreasi mengembangkan pemikirannya.
Pendekatan Matematika Realistik pertama kali dikembangkan oleh Institut Freudenthal di Negeri Belanda, berdasarkan pandangan Freudenthal. Ide utama dari pendekatan matematika realistik adalah siswa harus diberi kesempatan untuk menemukan kembali (reinvent) ide dan konsep matematika dengan bimbingan orang dewasa melalui penjelajahan berbagai situasi dan persoalan dunia nyata atau real world. Proses pengembangan konsep dan ide-ide matematika yang dimulai dari dunia nyata oleh De Lange dalam Saragih (2007:44) disebut matematisasi konsep dan memiliki model skematis proses belajar seperti pada Gambar di bawah ini:
Gambaran proses pengembangan konsep di atas tidak mempunyai titik akhir, hal ini menunjukkan bahwa proses lebih penting dari hasil akhir. Sedangkan titik awal proses menekankan pada konsepsi yang sudah dikenal siswa, hal ini disebabkan oleh asumsi bahwa setiap siswa memiliki konsep awal tentang ide-ide matematika. Setelah siswa terlibat secara bermakna dalam proses belajar, ia dapat ditingkatkan ke tingkat yang lebih tinggi untuk secara aktif membangun pengetahuan baru. Berkaitan dengan proses pengembangan konsep matematika di atas, menurut Gravemeijer dalam Saragih (2007:45) terdapat tiga prinsip utama dalam pendekatan matematika realistik yaitu: (a) Guided Reinvention and Progressive Mathematization (Penemuan terbimbing dan Bermatematika secara Progressif), (b) Didactical Phenomenology (Penomena Pembelajaran), dan (c) Self-developed Models (Pengembangan Model Mandiri).
Ketiga prinsip tersebut dapat dijelaskan secara singkat seperti yang dikemukakan Saragih (2007:45-46) sebagai berikut:
1. Prinsip Penemuan terbimbing dimaksudkan, siswa diberi kesempatan untuk menemukan sendiri konsep matematika dengan menyelesaikan berbagai soal kontekstual yang sudah dikenal siswa. Bermatematika secara progressif dimaksudkan bermatematika secara horizontal dan vertikal. Matematika secara horizontal, siswa diharapkan mampu mengidentifikasi soal kontekstual sehingga dapat ditransfer ke dalam soal bentuk matematika berupa model, diagram, tabel (model informal) untuk lebih dipahami. Sedangkan matematika vertikal, siswa menyelesaikan bentuk matematika formal atau non formal dari soal kontekstual dengan menggunakan konsep, operasi dan prosedur matematika yang berlaku.
2. Prinsip kedua, adanya penomena pembelajaran yang menekankan pentingnya soal kontekstual untuk memperkenalkan topik-topik matematika kepada siswa dengan mempertimbangkan: a) kecocokan aplikasi konteks dalam pembelajaran dan b) kecocokan dampak dalam proses penemuan kembali bentuk dan model matematika dari soal kontekstual tersebut.
3. Prinsip ketiga, pengembangan model mandiri berfungsi untuk menjembatani antara pengetahuan matematika non formal dengan formal dari siswa. Model matematika dimunculkan dan dikembangkan secara mandiri berdasarkan model-model matematika yang telah diketahui siswa. Di awali dengan soal kontekstual dari situasi nyata yang sudah dikenal siswa kemudian ditemukan model dari (model of) dari situasi tersebut (bentuk informal) dan kemudian diikuti dengan penemuan model untuk (model for) dari bentuk tersebut (bentuk formal), hingga mendapatkan penyelesaian masalah dalam bentuk pengetahuan matematika yang standar.
Sesuai dengan ketiga prinsip di atas, Saragih (2007:25) mengatakan, proses pembelajaran matematika di kelas berdasarkan pendekatan matematika realistik (PMR) perlu memperhatikan lima karakteristik yaitu: (1) menggunakan masalah kontekstual; (2) menggunakan model; (3) menggunakan kontribusi dan produksi siswa; (4) interaktif; dan (5) terintegrasi dengan topik pembelajaran lainnya.
Dalam pendekatan PMR, isi perangkat pembelajarannya mencerminkan tiga prinsip kunci PMR, dan proses implementasinya di kelas berpedoman pada 5 ciri yang disebutkan di atas.
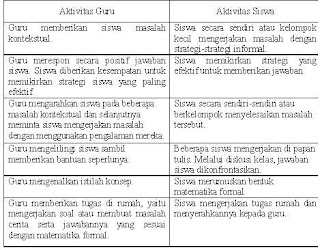
Adapun sintak implementasi matematika realistik adalah :
E. Penelitian Yang Relevan
Dari hasil penelitian yang dilakukan oleh Asrinovelisa Malihu (2006:39) mengungkapkan bahwa kemampuan belajar matematika siswa khususnya kemampuan hitung perkalian dan pembagian siswa kelas III SD Negeri 32 Poasia Kendari dapat ditingkatkan melalui Pendekatan Pembelajaran Matematika Realistik.
Dari hasil penelitian yang dilakukan oleh Sahat Saragih (2007:185) mengungkapkan bahwa Siswa Sekolah Menengah Pertama yang memperoleh pembelajaran berdasarkan pendekatan pembelajaran matematika realistik mempunyai kemampuan berpikir logis secara signifikan lebih baik dibanding siswa yang memperoleh pembelajaran berdasarkan pendekatan matematika secara biasa.
Dari hasil penelitian yang dilakukan oleh Kamiluddin (2007:48) menyimpulkan bahwa hasil belajar siswa kelas IV SD Negeri 8 Baruga Kendari pada pokok bahasan penjumlahan dan pengurangan pecahan dapat ditingkatkan melalui pendekatan RME.
F. Hipotesis Penelitian
Hipotesis yang akan diuji kebenarannya dalam penelitian ini adalah “Pendekatan Pembelajaran Matematika Realistik lebih efektif dibandingkan dengan Pendekatan Pembelajaran Konvensional dalam meningkatkan kemampuan penalaran matematika siswa”. Secara statistik hipotesis tersebut dapat dirumuskan sebagai berikut:
Keterangan : 1 = Rata-rata penalaran matematika siswa yang diajar dengan Pendekatan Pembelajaran Matematika Realistik.
2 = Rata-rata penalaran matematika siswa yang diajar dengan Pendekatan Pembelajaran Konvensional
Jumat, 17 Juli 2009
Efektivitas Pendekatan Pembelajaran Matematika Realistik Dalam Meningkatkan Kemampuan Penalaran Matematika Siswa Kelas VII SMP Negeri 8 Kendari
Langganan:
Posting Komentar (Atom)


0 komentar:
Posting Komentar